Buffering packets in a network with a variable source rate
As a natural extension my project hop, I decided to try and optimize it’s buffering technique. Here is the problem formalized a bit:
- A source which is capable of writing bytes at the rate of
S bytes/sec. - A network channel which can carry bytes at a bandwidth or rate of
B bytes/sec.Bis almost always slower thanS. - You can choose to read the data from the source slower than it can write, but that will cause delays.
- Maximum delay for any byte is bounded by the value
D. - To send
kbytes in an IP packet, you need to attach a header of sizeh. hdoes not depend onk, butkis limited to the size of an IP packet minush. Thus,kcan be expected to be around 65000 bytes at max.- An IP packet is received as an atomic entity. So
kchunked bytes will be received at the same time.
I tried to find an optimal solution for this, or a related problem. It turns out that this problem doesn’t even present a solution, and modifying the problem seems to help provide a workable problem. For the following section, I will assume that there is an added condition to the problem:
- You can afford to lose bytes at some rate.
With this information, I set on to try find something interesting in this problem (and end up using the found solution for another problem).
Note: Although assumed that the source can write at the speed of S bytes/sec, this will be considered only as an upper limit.
Losses are allowed
Here we are assuming (for the sake of keeping the problem well-defined) that the receiver does not mind random byte losses.
We first note a few key ideas regarding the optimal solution here:
- It is wasteful to not be using the network channel at any point of time. Better read and keep some bytes ready beforehand
- Sending too large chunks would increase delay
- Sending small chunks would cause the packet header size overhead to become significant
Async reading
We have 2 client side processes/threads. One of them handles reading from the input source, while the other handles writing to the network socket. For sake of convenience, we will now assume sr to be the speed of reading from the source asynchonously.
In the given scenario, this would follow:
- The last read
kbytes take $\frac{h+h}{B}$ time to be sent. - Meanwhile, the reader accumulates
kbytes to be sent once the above send is done. - While reading at the rate sr, this takes $\frac{k}{s_r}$ time.
- The remaining bytes written by the source during the time of send are lost.
- This loss time is $\frac{h+k}{B} - \frac{k}{s}$.
- These newly read bytes are sent once the previous send is finished.
Now we have the condition that any packet which reaches the receiver should not be too old (at max D seconds old). In that case, it is favorable to send only the packets read just before the next send (the most latest packets, since they are more valuable than the old ones). The figure describes this (green is reading from source, blue is sending over network):
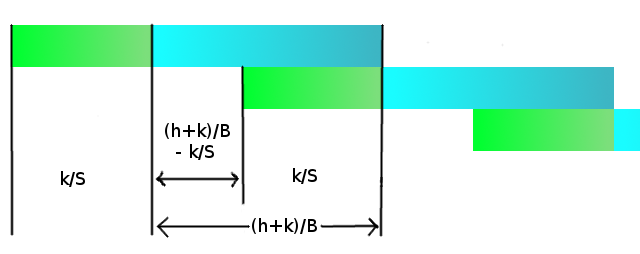
Now note that we are trying to minimize the losses, while keeping the delay in check. Total loss is N/k times the loss per k bytes, where N is the total amount of data to be sent (just an asymptotic constant for this case). We try find an expression for the total loss. Here, wasted means bytes which were not read, and thus never sent.
$$
wasted\ time\ per\ k\ bytes = \frac{h+k}{B} - \frac{k}{s_r}\\
wasted\ bytes\ per\ k\ bytes\ sent = (\frac{h+k}{B} - \frac{k}{s_r})\times s_r\\
total\ wastage\ in\ N\ bytes = (\frac{h+k}{B} - \frac{k}{s_r})\times s_r \times \frac{N}{k} \leq D
$$
Also
$$
delay\ of\ max\ delayed\ byte = \frac{h+k}{B} + \frac{k}{s_r} \leq D\\
\Rightarrow k \leq {D - \frac{h}{B}} \times \frac{Bs_r}{B+s_r}
$$
Using the constraint on k, we get:
$$
Wastage\ ratio = \frac{Wastage}{N} = (\frac{hs_r}{B} \times \frac{B+s_r}{DB-h}) + \frac{s_r - B}{B}
$$
This whole discussion assumed that old packets are considered useless. So our source should either find a way to not send packets for a while, or it should be robust enough to be able to tolerate some fractions of losses.
For Video streaming, one can envision a scenario where the source sends packets frame by frame, with the gap (the one we considered the loss) as a small fraction less than the frame gap in the desired frame rate.
Non-jerky data loss
Now what if it is surely a video stream, but we don’t want jerks in the data? (We’re still okay with losses). In that case, almost the whole analysis is the same as above, with the exception that now the oldest packet reaching the other side will not have been sent so late. The sending buffer will randomly drop packets with a probability of $1 - \frac{B}{h+k} \times \frac{k}{S}$. In the end, these packets will be sent over to the other side, but they will include packets close to the start of the blue region (above figure) too. So, the inequality for k will now be:
$$
delay\ of\ max\ delayed\ byte = 2\times\frac{h+k}{B} \leq D\\
\Rightarrow k \leq {\frac{DB}{2} - h}
$$
Of course, this will worsen our possible wastage ratio at a particular reading speed, since we increased the constraint on the delay.
Losses are NOT allowed
Using the above section’s results (The jerky data loss), we can actually get a solution such that the wastage is 0 (for the case when data is transmitted jerkily).
We need to slow down the sender quite a bit though:
$$s_r = B - \frac{2h}{D}$$
So if it is possible to slow down the sender this much (or simply read slowly, helpful in cases when you’re basically sending bytes written by a human, or sending a file), we know how fast we can afford to read. Of course, we could have solved this taking delay as 0 right from the start, but that would deprive us of the observations in the previous section :smile:
Conclusion
Already having spent quite a bit on this article (and now wanting to go back to my other ideas related to networks), I’ll leave this post here, unfinished. There can be quite a few conclusions from this, which would possibly have been written down in some paper or the other for sure. But I believe being so nascent in this field, trying out things on your own has its own charm! Will probably work some more on this if I get time.